線形的増加と指数関数的増加
曽呂利新左衛門、という人物の名前をご存知でしょうか。
豊臣秀吉の家来で、落語家の始祖とも言われる人物だそうです。トンチが効いたやりとりが得意で、面白いことが大好きな秀吉がいかにも好みそうな人物ですね。
今回のお話は、曽呂利新左衛門と秀吉の次のような有名なエピソードに関係したものです。
手柄を立てた新左衛門に、秀吉は褒美を与えようとして、何でも欲しいものを言えと彼に言います。すると新左衛門は、「1日目は米1粒、その次の日はその2倍、次の日は2日目の2倍、のようにして100日間お与えください。」と応じました。
秀吉はなんと欲のない奴だと思ったことでしょう。米が1粒2粒と増えたところで、100日後なんて大した数にもならないだろうにと。秀吉はその希望を叶えてやることにしましたが、しばらく後に大変な約束をしてしまった、と後悔をすることになります。
物事が増えていく様子を、人間は直感的に同じ調子で増えていくと捉えがちです。1日後は2粒、2日後は4粒、3日後は6粒、4日後は8粒・・・のように、1日に2粒ずつ増えるような増え方です。増え方に変化がありません。これを「線形的増加」と言います。
それに対して新左衛門が出した条件での増え方は、増え方自体が増えるように、つまり加速して増えていくものです。これを「指数関数的な増加」と言います。2日目は1日目の2倍、次の日は2倍の2倍で4倍に、次の日は4倍の2倍で8倍に、次の日は8倍の2倍で16倍に増えていきます。この時点なら、まだ16倍です。大したことはないように思うでしょうか。10日後は1,024粒、20日後は1,048,576粒と100万粒を超え、30日後は1,073,741,824粒と10億粒を超えます。それに気がついた秀吉は、別の希望に変えてくれとお願いしたそうです。
仮に、線形的に増える方の関数を\(y=2x\)、指数関数の方を\(y=2^x\)としてグラフを描いてみましょう。\(x\)の範囲を\(0\le x \le 3\)にしました。
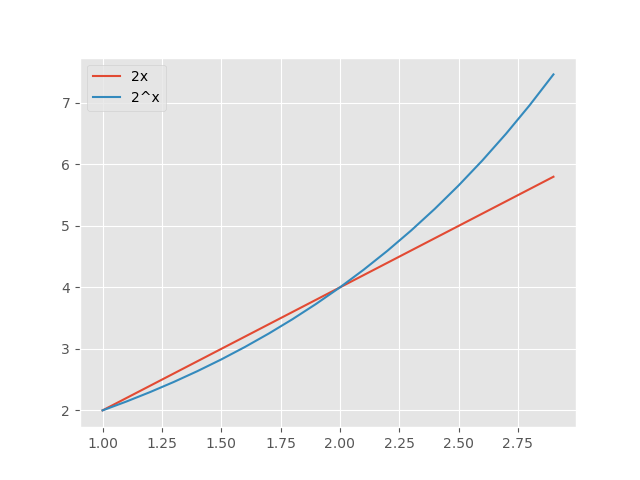
これを見ると、1から2までの範囲では線形関数の方が優っています。それ以降は指数関数がすごい勢いで追い抜いていく様子がよくわかります。
\(0\le x \le 8 \)の範囲ならどうなるか見てみましょう。
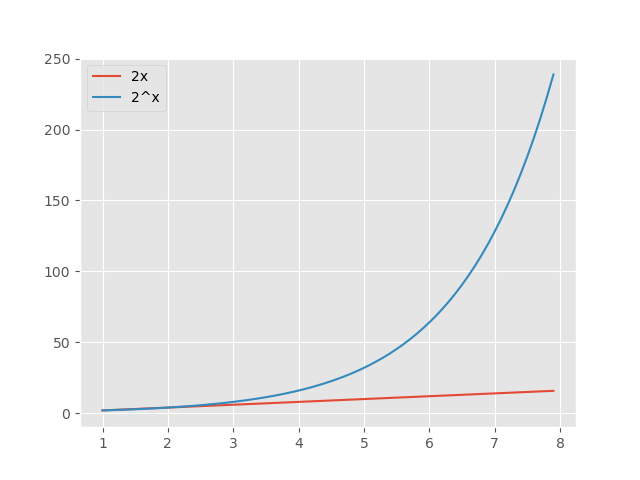
指数関数の増え方がいかに圧倒的かよくわかります。他に気がつく点はないでしょうか。縦のメモリが50倍のスケールに変わっていて、線形グラフが図の底の方に追いやられてしまいました。指数関数と線形関数とでは、同じグラフに表すのにはスケールが違いすぎるのです。さらに、横軸のメモリ3くらいまでは、指数関数も線形関数も対して変わらないように見えます。秀吉が直感的に大したことはないと思った原因がここにあるのかもしれません。人間は自分の手の届く範囲で空間や時間を把握することに慣れていてはいるけれど、大きなスケールで物事を捉えるのが苦手なのかもしれません。上の図のような横軸のメモリ幅はほとんど変わらないのに、縦のメモリの幅が急激に変化するようなものを想像するのは、よほど慣れていないと難しいでしょう。
自然現象に現れる複利効果
前回のお話しに、72の法則というのがありました。そこで出てきた「複利で増える」という条件が、今回の指数関数的増加にそのまま当てはまるものです。株式や投資信託など金融商品の多くがこうした数学的仕組みを期待して作られています。
複利で増える仕組みを持つ現象にはどんなものがあるか、いくつか書き出してみましょう。
- 生物の増殖:
例えば細胞の分裂や繁殖では、1つの細胞が2つになり、その2つがさらに分裂することで指数関数的に増加します。これは複利の原理と類似しています。 - 知識やスキルの累積:
人間の知識やスキルも、学習や経験の積み重ねにより、初めの基礎的な理解や能力が次の学習の土台となり、それがさらに高度な知識やスキルの習得を促進します。これも一種の複利的な増加です。 - ネットワーク効果:
ソーシャルネットワークやテクノロジーにおいても、ユーザーが増えることでそのネットワークの価値が指数関数的に増加することがあります。これは、各新規ユーザーが既存のユーザー全体の価値を増加させるためです。 - 資本の再投資:
金融の世界では、得られた利息や収益が再び投資されることで、次の期間には元本が増加し、その元本に対して再び利息がつきます。これにより、元本が雪だるま式に増加します。
ある量が増加するたびに、その増加分もまた次の増加の基礎になる。そうした共通点が上に挙げた例にはあるようです。
私たち人間は、複利的に増える仕組みを持つ細胞から成り立っています。それが全ての起点になっているように見えます。テクノロジーの発明と発展、ネットワークの構築、企業活動に対する資本の投入、これらは全て人間活動の表れです。それらが複利的に増加する傾向があるのも頷けます。
学習に活かす
これらの現象についての理解が、今後の取るべき行動の指針に深く関わっていくような気がします。例えば受験生や、資格やスキル取得に取り組んでいる人であれば、例の2番目「知識やスキルの累積」に着目したいですね。
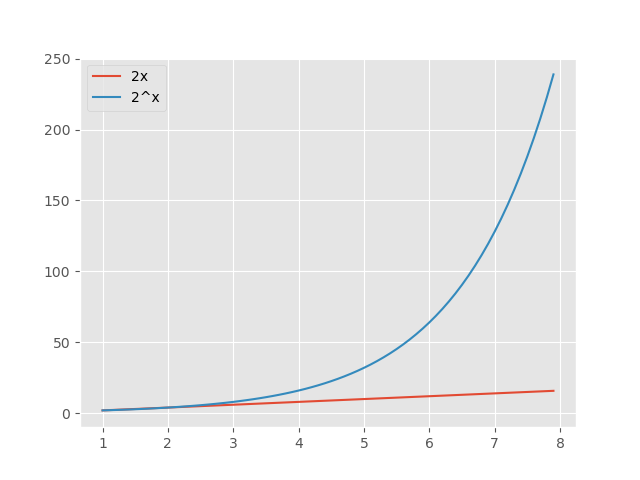
もう一度掲載しましたが、上のグラフを次のように見るのも面白いかもしれません。
学習に取り組む時間経過に着目してみましょう。学習開始から1ヶ月から3ヶ月経過しても何も変化がなく、成果が現れないように思います。実に多くの人がこの期間中に脱落してしまうのです。成果が出にくい魔の期間です。しかしそれを乗り越えて、4ヶ月、5ヶ月ほどしてくると目に見えて成果が現れています。7ヶ月、8ヶ月もすると膨大な量に増えています。
あるいは、反復回数に着目するとどうでしょう。例えば大変難しい問題集に取り組んでいるとします。1回や2回程度の復習ではほとんど変化がありません。それが5往復、7往復としていけば急速に「完全な理解」へと近づいていくのがわかります。よく「問題集は3回繰り返せば良い」と言いますが、マスターするのが難しい問題集については、それでは足りないようです。「7回以上繰り返せば、確実にモノになる」というのが正しいようです。
期間で7ヶ月以上、反復回数は7回以上の学習法で、確実にマスターできるのです。
今までなら「自分には絶対無理だ」と諦めていたであろう分野の勉強だったり、苦手だと思い込んでいた科目に対する向き合い方が、これで変わるはずです。
よく「自分は文系だから数学は苦手で」という人がいます。しかし数学を学んでいた時の自分をよく思い出してみると、成果が出にくい魔の期間に勉強から離脱していたのかもしれません。上のグラフのように、上手に複利効果を利用した学習法を取り入れて、「理解できる快感」を繰り返し味わっていけば、それが辛い勉強に向かうモチベーションを維持する原動力になるはずです。入り口は辛くて嫌な勉強ですが、出口には最上の喜びが待っているという仕組みですね。
かつて学生時代の勉強に挫折して、長い年月学ぶことから離れていた人でも、複利効果を意識してまた初めからやり直せば、確実に目標に到達できるということです。例えば「相対性理論」のような、なかなか手が出にくそうな難しい分野の理解にも、誰でも必ず到達できるということです。そういえばあのアインシュタインも、複利は人類最大の発明だ、といったそうです。